1. 나머지 연산
- 덧셈 : (A+B)modM = ((AmodM)+(BmodM))modM
- 곱셍 : (A*B)modM = ((AmodM)*(BmodM))modM
- 뺄셈 : (A-B)modM = ((AmodM)-(BmodM)+M)modM
cf) 왜 덧셈, 곱셈과 달리 +M을 해주는가?
ex) ((6%3)-(5%3))%3 = -2%3 = ?
이 답은 -2인가 1인가 -> 언어마다 답이 다르다. (Java, C는 -2, Python은 1이라고 답함)
이를 방지하기 위해 값이 음수로 나와도 이를 양수로 바꾸고 연산하기 위해 +M을 해주는 것임.
2. 최대공약수 GCD(Greatest Common Divisor), 최소공배수(Least Common Multiple)
int gcd = 1;
for (int i=2;i<min(a,b);i++) {
if ((a%i == 0) && (b%i == 0)) {
g = i;
}
}작은 수부터 큰 수로 순서로 구하므로 최종적으로 구해진 공약수(gcd)는 최대공약수가 된다.
O(N)의 시간이 걸리는 알고리즘
# 유클리드 호제법
GCD(a, b) = GCD(b, r)
이 때, r은 a를 b로 나눈 나머지이다.
r = 0이 될때, b가 최대공약수가 된다.
ex) GCD(24, 16) = GCD(16, 8) = GCD(8, 0) -> 최대공약수 = 8
public int gcd(int a, int b) {
if (b==0) { // r이 0이 된 상황 -> 이때 a 자리의 수가 최대공약수가 된다.
return a;
} else{
return gcd(b, a%b); // 재귀함수를 사용하여 최대공약수가 나올때까지 연간
}
}public int gcd(int a, int b) { // 재귀함수를 사용하지 않은 유클리드 호제법
while (b != 0) {
int r = a%b;
a = b;
b = r;
}
return a;
}O(logM)의 시간이 걸리는 알고리즘
최소공배수는 최대공약수를 이용하여 구할 수 있다.
LCM = GCD*(a/GCD)*(b/GCD) 이다.
3. 소수 (중요)
대표적으로 두가지 알고리즘이 존재한다.
1) 어떤 수 N이 소수인지 아닌지 판별하는 알고리즘
2) 어떤 수 N보다 작거나 같은 모든 자연수 중에서 모든 소수들을 찾아내는 알고리즘
1) 어떤 수 N이 소수인지 아닌지 판별하는 알고리즘
public class Main {
public boolean prime(int n) {
if (n < 2) { // 2보다 작은 소수는 없음
return false;
}
for (int i=2;i<n-1;i++) {
if (n%i == 0) { // 나누어 떨어지는 수가 있으면
return false; // 소수 아님
}
}
return true; // 위 판정을 통과하면 소수가 맞음 (나누어떨어지는 수가 없었음)
}
}위 알고리즘은 O(N)의 시간이 걸린다.
N이 소수가 되기 위해서는 2보다 크거나 같고 N/2보다 작거나 같은 자연수로 나누어 떨어지면 안된다.
이는 N에 대해 N/2보다 큰 수로는 절대 나누어 떨어지지 않는다는 것을 의미하기도 한다.
이를 활용하면
public class Main {
public boolean prime(int n) {
if (n < 2) { // 2보다 작은 소수는 없음
return false;
}
for (int i=2;i<n/2;i++) { // n/2보다 큰 수로는 나누어떨어지지 않는다는 것을 알기 때문에 n/2까지만 확인
if (n%i == 0) { // 나누어 떨어지는 수가 있으면
return false; // 소수 아님
}
}
return true; // 위 판정을 통과하면 소수가 맞음 (나누어떨어지는 수가 없었음)
}
}이렇게 O(N/2)의 알고리즘을 만들 수 있다. (하지만 O(N/2)도 결국은 O(N)..)
N이 소수가 아니라면, N = a*b꼴로 나타낼 수 있다. (이 때, a, b >= 2이다.)
a<=b이라고 할 때, a<루트(N), 루트(N)<b이다.
ex) 24의 약수에는 1, 2, 3, 4, 6, 8, 12, 24가 있다. 여기서 a = 1,2,3,4 / b = 6,8,12,24
루트(N) = 4.xxx -> a < 4.xxx, 4.xxx < b
이에 따라 루트(N)까지만 검사를 해보면 N이 소수인지 판단할 수 있다.
public class Main {
public boolean prime(int n) {
if (n < 2) { // 2보다 작은 소수는 없음
return false;
}
// 실수는 근사값이므로 사용하지 않는 것이 좋기 때문에 i<=루트(n) 대신 i*i<=n을 사용
for (int i=2;i*i<=n;i++) { // 루트(n)까지만 검사를 하는 것.
if (n%i == 0) { // 나누어 떨어지는 수가 있으면
return false; // 소수 아님
}
}
return true; // 위 판정을 통과하면 소수가 맞음 (나누어떨어지는 수가 없었음)
}
}O(루트(N))의 시간이 걸리는 알고리즘
2) 어떤 수 N보다 작거나 같은 모든 자연수 중에서 모든 소수들을 찾아내는 알고리즘
1번의 알고리즘을 활용한다.
N을 기준으로 같거나 작은 소수를 구하려면, N개의 숫자에 대해 루트(N)이 걸리는 1번의 알고리즘을 사용해야 한다.
-> O(N루트(N))의 시간이 걸리는 알고리즘
이보다 빠른 방법은 에라토스테네스의 체를 사용한 방법이 있다.
소수를 구하기 위한 가장 바람직한 방법 중 하나이다.
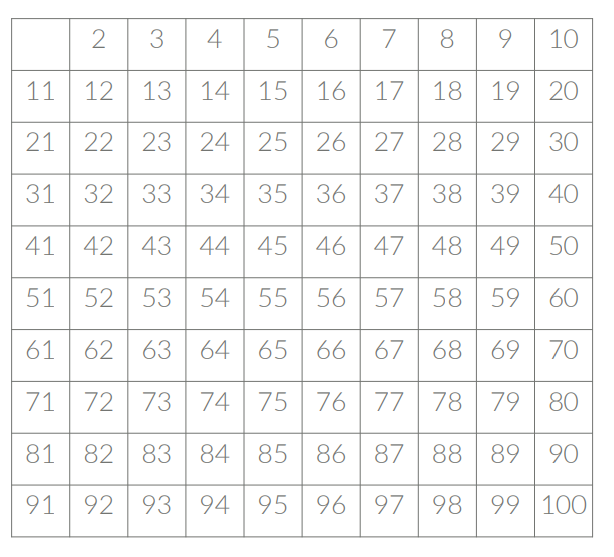
좌측의 표를 사용한다. (N=100 가정)
먼저, 지워지지 않은 수 중 가장 작은 수는 2이다.
그럼 2는 소수가 된다.
그리고 2의 배수는 모두 소수가 아니기 때문에 표에서 전부 지워준다.
이렇게 지워지지 않은 수 중 가장 작은 수를 구하고, 그 수의 배수들을 전부 지우는 과정을 반복 수행하면 소수들을 구할 수 있다.
(해당 경우에서는 10번 반복)
(11*11 = 121 > 100이기 때문)

10번의 과정 반복을 통해 소수를 제외한 수들을 모두 제거한 모습이다.
public class Main {
int[] prime = new int[100];
int pn = 0; // 소수의 개수
boolean[] check = new boolean[101]; // 소수가 아닌수가 지워지면 해당 칸을 true로 함 (boolean 초기 값은 false임)
int n = 100;
for (int i=2;i<=n;i++){
if (check[i] == false) {
prime[pn++] = i;
for (int j=i*i;j<=n;j+=i) { // i*i는 n의 크기에 따라 i+i 또는 i*2로 바꾸는 것이 바람직하다.
// 그러나 n의 크기가 작다면 i*i가 더 빠름
// (i*i보다 작은 i의 배수들은 이미 i보다 작은 소수들의 배수에 의해 지워졌기 때문에 따로 처리할 필요가 없음)
// i = 백만이면 int의 범위를 넘어가버리기 때문이다.
check[j] = true;
}
}
}
}
수를 실제 배열세어 실제로 지우려하면 시간이 오래 걸리므로 새로운 check 배열을 사용해서 제거 표시
O(NloglogN)의 시간이 걸리는 알고리즘
cf) 골드바흐의 추측
- 2보다 큰 모든 짝수는 두 소수의 합으로 표현 가능하다.
- 5보다 큰 모든 홀수는 세 소수의 합으로 표현 가능하다. (위의 명제에 3을 더한 것)
아직 완전히 증명되지 않았다. (10의 18제곱 까지는 참이라고 증명이 되었다.)
4. 팩토리얼
팩토리얼은 매우 큰 값이다.
- 팩토리얼 0의 개수 구하기
N!에서 0의 개수를 구하는 문제
ex) 10! = 3620 -> 2개
이 이유는 10!을 소인수분해 해보면 알 수 있다. -> 0을 만들 수 있는 소인수는 10과 2*5밖에 없다. (각각 1개씩 있으므로 0은 총 2개)
5의 개수가 항상 2의 개수보다 적기 때문에 5의 개수만 세어주면 소수의 개수를 알아낼 수 있다.
(인수로 5가 들어가는 숫자 세어주기)
-> 100을 기준으로
100/5 = 20 : 젓어도 5가 1개 들어가는 인수 20개 나옴
100/25 = 4 : 적어도 5가 2개 들어가는 인수 4개 나옴
따라서 100!의 0의 개수는 20+4 = 24로 24개이다.
'알고리즘' 카테고리의 다른 글
| 알고리즘) 트리(Tree) (0) | 2020.08.17 |
|---|---|
| 알고리즘) 그래프의 탐색 - DFS, BFS (0) | 2020.08.17 |
| 알고리즘) 그래프(Graph) (0) | 2020.08.17 |
| 알고리즘)브루트 포스(Brute Force)와 순열(permutation) (0) | 2020.08.05 |
| 알고리즘) 다이나믹 프로그래밍(Dynamic Programming)이 무엇인가? (0) | 2020.07.20 |
알고리즘 카테고리의 다른 글
알고리즘) 그래프의 탐색 - DFS, BFS
2020.08.17알고리즘) 그래프(Graph)
2020.08.17알고리즘)브루트 포스(Brute Force)와 순열(permutation)
2020.08.05알고리즘) 다이나믹 프로그래밍(Dynamic Programming)이 무엇인가?
2020.07.20